归并排序

发表于 | 分类于 ，
字数统计: | 阅读时长 ≈

归并排序

归并排序基本原理是合并两个已排序的数组
https://www.cnblogs.com/chengxiao/p/6194356.html

递归实现，自顶向下,between top down merge: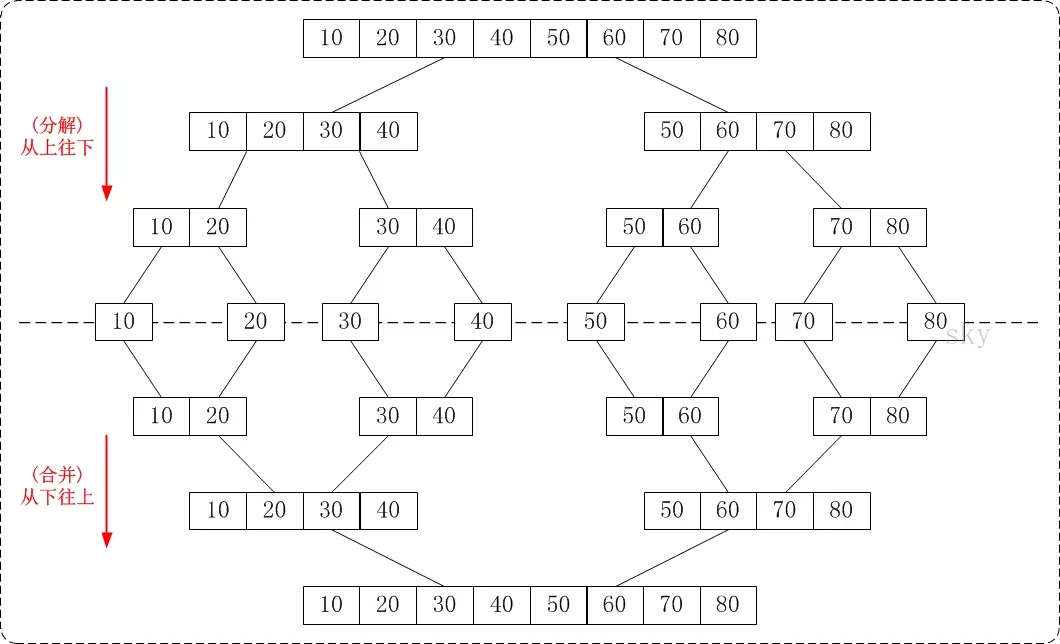

非递归,自底向上,bottom up merge sort: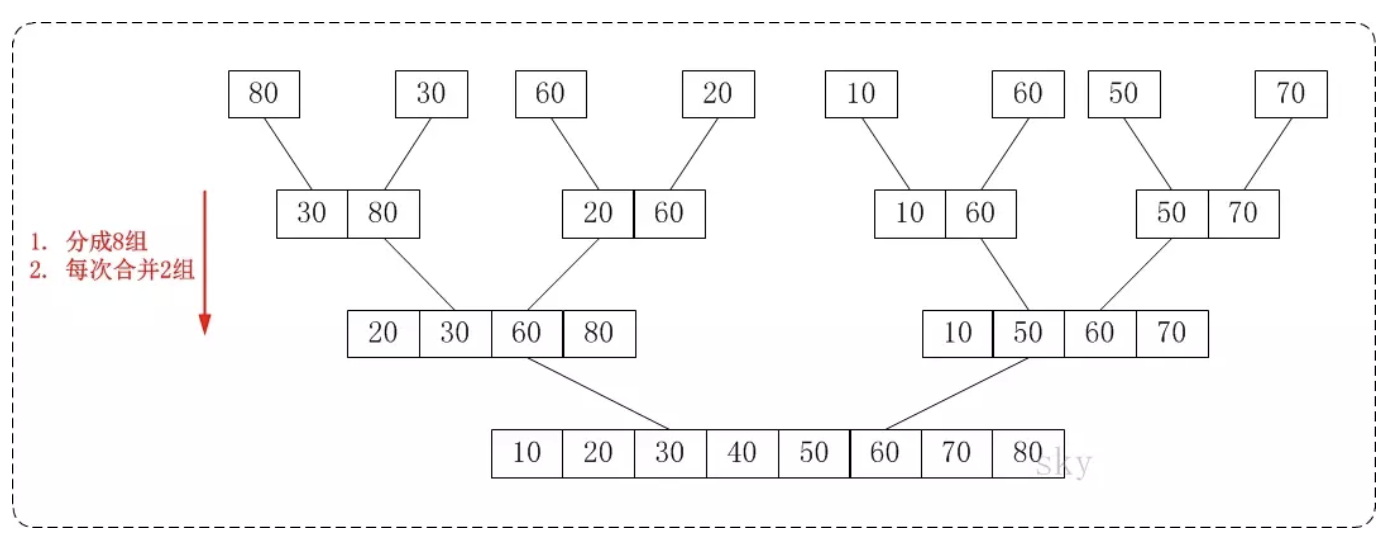

递归就是把大问题拆解成一个个小问题,最后拆成两两相邻元素比较.

java实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
package cn.llnn.sort;

import java.util.Arrays;

/**
 * 归并排序
 *
 * @author llnn
 * @create 2019-09-23 21:47
 **/
public class MergeSort {

    private static void merge(int[] a, int low, int mid, int high) {
        int[] temp = new int[high - low + 1];
        int l = low;
        // 这里为什么要加1
        int h = mid + 1;
        int k = 0;
        // 为什么要小于等于
        while (l <= mid && h <= high) {
            if (a[l] < a[h]) {
                temp[k++] = a[l++];
            } else {
                temp[k++] = a[h++];
            }

        }
        // 因为要遍历到最后一个元素,所以是小于等于
        while (l <= mid) {
            temp[k++] = a[l++];
        }
        while (h <= high) {
            temp[k++] = a[h++];
        }
        if (temp.length >= 0) {
            System.arraycopy(temp, 0, a, low, temp.length);
        }
        System.out.println(Arrays.toString(a));
    }

    private static void mergeSort(int[] a, int low, int high) {
        /*
          递归实现，自顶向下,between top down merge
         */
        if (low >= high) {
            return;
        }
        int mid = (low + high) / 2;
        // 为啥high是mid,不是mid -1
        mergeSort(a, low, mid);
        mergeSort(a, mid + 1, high);
        merge(a, low, mid, high);
    }

    private static void mergeSort2(int[] a) {
        /*
          非递归,自底向上,bottom up merge sort
         */
        int N = a.length;
        /* 第一层循环 表示归并排序子数组的长度 从1 , 2 , 4 ,8 ..... */
        for (int sz = 1; sz < N; sz *= 2) {
            System.out.println("sz" + sz);
            //第二层循环表示每两个自数组之间归并排序，确定起始和终止INDEX
            for (int lo = 0; lo < N - sz; lo += 2 * sz) {
                System.out.println("low:" + lo + "mid" + (lo + sz - 1) + "high" + Math.min(lo + 2 * sz - 1, N - 1));
                merge(a, lo, lo + sz - 1, Math.min(lo + sz + sz - 1, N - 1));
            }
        }
    }

    public static void main(String[] args) {
        int[] a = {51, 46, 20, 18, 65, 97, 82, 30, 77, 50};
        mergeSort(a, 0, a.length - 1);
//        mergeSort2(a);
        System.out.println("排序结果：" + Arrays.toString(a));
    }

}

python实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

def merge(arr, low, mid, high):
    l = low
    h = mid + 1
    temp = []

    while l <= mid and h <= high:
        if arr[l] < arr[h]:
            temp.append(arr[l])
            l += 1
        else:
            temp.append(arr[h])
            h += 1

    while l <= mid:
        temp.append(arr[l])
        l += 1
    while h <= high:
        temp.append(arr[h])
        h += 1
    for i in temp:
        arr[low] = i
        low += 1
    print(arr)


def merge_sort(arr, low, high):
    # 为啥是大于等于
    if low >= high:
        return
    mid = int((low + high) / 2)
    # 为啥high是mid,不是mid-1
    merge_sort(arr, low, mid)
    merge_sort(arr, mid + 1, high)
    merge(arr, low, mid, high)
    pass


def merge_sort1(arr):
    size = 1
    while size < len(arr):
        low = 0
        while low < len(arr) - size:
            high = min(2 * size + low - 1, len(arr) - 1)
            mid = low + size - 1
            merge(arr, low, mid, high)
            low += 2 * size
        size = 2 * size


if __name__ == '__main__':
    arr = [51, 46, 20, 18, 65, 97, 82, 30, 77, 50]
    # merge_sort(arr, 0, len(arr) - 1)
    merge_sort1(arr)
    print(arr)

边界界定:

非递归方法,边界界定:

  1. 让相邻的两个数组进行归并,保证相邻的两个元素是有序的.
  2. 由于相邻两个数组变成有序了,所以子数组长度是按2的指数增长的1,2,4,8…
  3. 需要找出low,mid,high 之前的关系

递归方法:

参考:

https://www.cnblogs.com/edwinchen/p/4783218.html
https://blog.csdn.net/MoreWindows/article/details/6678165
https://blog.csdn.net/jianyuerensheng/article/details/51262984
bottom up merge sort