gc

发表于 2019-12-18 | 分类于 go

字数统计: | 阅读时长 ≈

如何打开gc日志

go version
go version go1.13.1 linux/amd64

gc日志解释

手动gc

debug.FreeOSMemory() vs runtime.GC()

通过pprof

疑问

gc后内存是否归还
不要频繁调用gc

常见的坑

发表于 2019-12-16 | 分类于 go

字数统计: | 阅读时长 ≈

tip

go 捕获协程中的panic

goroutine发生panic，只有自身能够recover，其它goroutine是抓不到的

package test

import (
	"fmt"
	"testing"
	"time"
)

func Test_Panic(t *testing.T) {
	defer func() {
		if r := recover(); r != nil {
			fmt.Println("out捕获到的错误", r)
		}
	}()
	go func() {
		fmt.Println("hello")
		time.Sleep(time.Second)
		panic("error")
	}()
	time.Sleep(time.Hour)
}

如上是不能捕获到异常的,需要如下处理在协程中捕获

package test

import (
	"fmt"
	"testing"
	"time"
)

func Test_Panic(t *testing.T) {
	defer func() {
		if r := recover(); r != nil {
			fmt.Println("out捕获到的错误", r)
		}
	}()
	go func() {
		defer func() {
			if r := recover(); r != nil {
				fmt.Println("in捕获到的错误：", r)
			}
		}()
		fmt.Println("hello")
		time.Sleep(time.Second)
		panic("error")
	}()
	time.Sleep(time.Hour)
}

raft思考

发表于 2019-12-14 | 分类于 raft

字数统计: | 阅读时长 ≈

https://www.zhihu.com/question/54997169

问题:

客户端怎么感知leader切换?
最简单的方法非leader收到请求回复客户端自己不是leader
raft成员变更
raft里最麻烦的应该是成员变更,简单点就一个个加,实现起来有些麻烦，启动时还得从快照和日志里捞成员
raft集群节点与允许故障个数:

3个节点最多允许挂1个,因为投票节点需要至少2个
4个节点最多允许挂1个,因为投票节点需要至少3个
5个节点最多允许挂2个,因为投票节点需要至少3个

etcd raft实现

发表于 2019-12-13 | 分类于 etcd

字数统计: | 阅读时长 ≈

https://zhuanlan.zhihu.com/p/49792009

Raft

发表于 2019-12-10 | 分类于论文

字数统计: | 阅读时长 ≈

Raft一致性算法

Raft 协议是一个分布式共识(consensus)算法, 可以参考 ATC-Raft 和 Thesis-Raft 这两篇文章. 两篇文章是同一个作者, 第一篇是小论文, 第二篇是大论文, 阐释地更加全面、详细

5.3 日志复制

5.4 安全性

任何领导人对于给定的任期号,都拥有了之前任期的所有被提交的日志条目.

5.4.1 选举限制

前提是:领导人都必须存储所有已经提交的日志条目

在任何基于领导人的一致性算法中，领导人都必须存储所有已经提交的日志条目,在某些一致性算法中,通过某些补偿机制将丢失的日志条目并把他们传送给新的领导人,raft增加了选举限制,保证领导人日志的完整性.这意味着日志条目的传送是单向的，只从领导人传给跟随者，并且领导人从不会覆盖自身本地日志中已经存在的条目
请求投票 RPC 实现了这样的限制： RPC 中包含了候选人的日志信息，然后投票人会拒绝掉那些日志没有自己新的投票请求。
Raft 通过比较两份日志中最后一条日志条目的索引值和任期号定义谁的日志比较新。如果两份日志最后的条目的任期号不同，那么任期号大的日志更加新。如果两份日志最后的条目任期号相同，那么日志比较长的那个就更加新。

通过选举策略实现

5.4.2 提交之前任期内的日志条目

Raft算法保证所有已提交的日志条目都是持久化的,只要一条记录被复制到大多数机器上,领导人就能提交.

领导人宕机会有如下几种情况:

领导人在将日志记录保存到大多数服务器上时已经提交后宕机
领导人在将日志记录保存到大多数服务器但是还没来得及提交时宕机
领导人还没有将日志记录保存到大多数服务器上时宕机

对于2,3情况,日志被覆盖并没有什么问题,但是对于1,日志被覆盖就会丢数据出现问题.如下展示了一种情况，一条已经被存储到大多数节点上的老日志条目，也依然有可能会被未来的领导人覆盖掉

在 (a) 中，S1 是领导者，部分的复制了索引位置 2 的日志条目。
在 (b) 中，S1 崩溃了，然后 S5 在任期 3 里通过 S3、S4 和自己的选票赢得选举，然后从客户端接收了一条不一样的日志条目放在了索引 2 处
然后到 (c)，S5 又崩溃了；S1 重新启动，选举成功，开始复制日志。在这时，来自任期 2 的那条日志已经被复制到了集群中的大多数机器上，但是还没有被提交
如果 S1 在 (d) 中又崩溃了，S5 可以重新被选举成功（通过来自 S2，S3 和 S4 的选票），然后覆盖了他们在索引 2 处的日志
反之，如果在崩溃之前，S1 把自己主导的新任期里产生的日志条目复制到了大多数机器上，就如 (e) 中那样，那么在后面任期里面这些新的日志条目就会被提交（因为S5 就不可能选举成功）

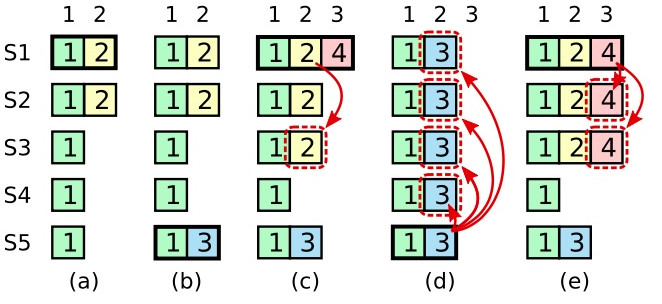
所以综上,领导人无法决定是否对老任期号的日志条目进行提交.Raft为了简化问题使用一种更加保守的方法,引入任期号的概念

任期内提交的数据时,至少复制到多数机器时才能提交
无论上一个任期数据有没有提交,都会复制过来(保留之前的任期号),然后本任期内产生的日志的任期号都会加1(这不是存在多数据的问题?)

5.4.3 安全性论证

反证法是“间接证明法”一类，是从反方向证明的证明方法，即：肯定题设而否定结论，经过推理导出矛盾，从而证明原命题; 接下来通过反证法来证明领导人的完全特性(任何领导人对于给定的任期号,都拥有了之前任期的所有被提交的日志条目)

假设任期 T 的领导人（领导人 T）在任期内提交了一条日志条目，但是这条日志条目没有被存储到未来某个任期的领导人的日志中(假设大于T的最小任期U的领导人U没有这条日志条目)

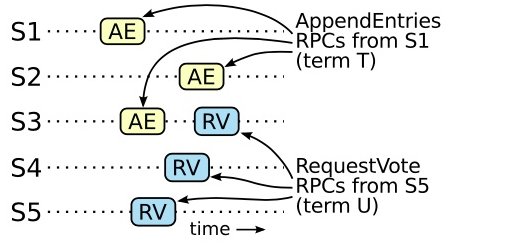
图9: S1,S2,S3,S4,S5是5台机器,如果 S1 （任期 T 的领导者）提交了一条新的日志在它的任期里，然后 S5 在之后的任期 U 里被选举为领导人，然后至少会有一个机器，如 S3，既拥有来自 S1 的日志，也给 S5 投票了。

在领导人 U 选举的时候一定没有那条被提交的日志条目（领导人从不会删除或者覆盖任何条目）。
领导人 T 复制这条日志条目给集群中的大多数节点，同时，领导人U 从集群中的大多数节点赢得了选票。因此，至少有一个节点（投票者、选民）同时接受了来自领导人T 的日志条目，并且给领导人U 投票了，如图 9这个投票者是产生这个矛盾的关键。
这个投票者必须在给领导人 U 投票之前先接受了从领导人 T 发来的已经被提交的日志条目；否则他就会拒绝来自领导人 T 的附加日志请求（因为此时他的任期号会比 T 大）。
投票者在给领导人 U 投票时依然保存有这条日志条目，因为任何中间的领导人都包含该日志条目（根据上述的假设），领导人从不会删除条目，并且跟随者只有在和领导人冲突的时候才会删除条目。
投票者把自己选票投给领导人 U 时，领导人 U 的日志必须和投票者自己一样新。这就导致了两者矛盾之一。
首先，如果投票者和领导人 U 的最后一条日志的任期号相同，那么领导人 U 的日志至少和投票者一样长，所以领导人 U 的日志一定包含所有投票者的日志。这是另一处矛盾，因为投票者包含了那条已经被提交的日志条目，但是在上述的假设里，领导人 U 是不包含的。
除此之外，领导人 U 的最后一条日志的任期号就必须比投票人大了。此外，他也比 T 大，因为投票人的最后一条日志的任期号至少和 T 一样大（他包含了来自任期 T 的已提交的日志）。创建了领导人 U 最后一条日志的之前领导人一定已经包含了那条被提交的日志（根据上述假设，领导人 U 是第一个不包含该日志条目的领导人）。所以，根据日志匹配特性，领导人 U 一定也包含那条被提交的日志，这里产生矛盾。
这里完成了矛盾。因此，所有比 T 大的领导人一定包含了所有来自 T 的已经被提交的日志。
日志匹配原则保证了未来的领导人也同时会包含被间接提交的条目，例如图 8 (d) 中的索引 2。

5.5跟随者和候选人崩溃

如果跟随者或者候选人崩溃了，那么后续发送给他们的 RPCs 都会失败。Raft 中处理这种失败就是简单的通过无限的重试
如果崩溃的机器重启了，那么这些 RPC 就会完整的成功。如果一个服务器在完成了一个 RPC，但是还没有响应的时候崩溃了，那么在他重新启动之后就会再次收到同样的请求。Raft 的 RPCs 都是幂等的，所以这样重试不会造成任何问题

5.6 时间和可用性

领导人选举是 Raft 中对时间要求最为关键的方面。Raft 可以选举并维持一个稳定的领导人,只要系统满足下面的时间要求：

广播时间（broadcastTime） << 选举超时时间（electionTimeout） << 平均故障间隔时间（MTBF）

广播时间必须比选举超时时间小一个量级，这样领导人才能够发送稳定的心跳消息来阻止跟随者开始进入选举状态；
通过随机化选举超时时间的方法，这个不等式也使得选票瓜分的情况变得不可能。
选举超时时间应该要比平均故障间隔时间小上几个数量级，这样整个系统才能稳定的运行。当领导人崩溃后，整个系统会大约相当于选举超时的时间里不可用；我们希望这种情况在整个系统的运行中很少出现。

集群成员变化

集群节点变更是很常见的需求,例如移除故障或者增加节点,首先来思考这个过程中会遇到什么问题?

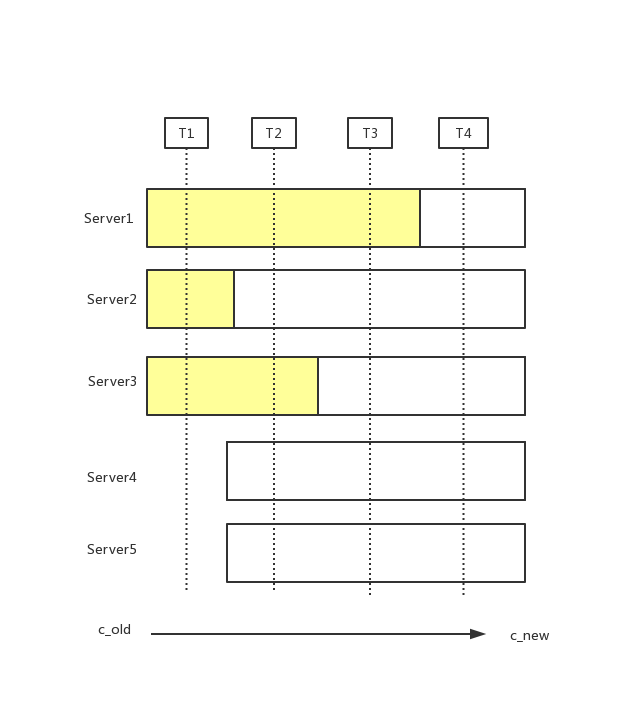
这里把[server1,server2,server3] 叫做c_old,[server1,server2,server3,server4,server5] 叫做c_new
集群从c_old状态变成c_new状态,在不停c_old服务情况下,会有一个节点同时给c_old集群中的发送变更消息,通知server更新自己的配置,由于分布式服务,各个server应用通知存在时间差,就会存在如上图情况.

存在这样的一个时间点，两个不同的领导人在同一个任期里都可以被选举成功。一个是通过旧的配置，一个通过新的配置,例如server5通过server3,server4,server5投票选举成leader,3个选票超过新配置总数5的一半, server1 通过server1,server2投票选举成leader,2个选票超过老配置3的一半

分布式情况中协调多个节点进行同一操作,最容易想到的最简单的就是2PC(两阶段提交),但这样其实是有问题的，先不说 2 PC 一些 corner case 需要处理，整个过程还可能会导致暂时的服务不可用，虽然这个时间在多数情况下面可能比较短

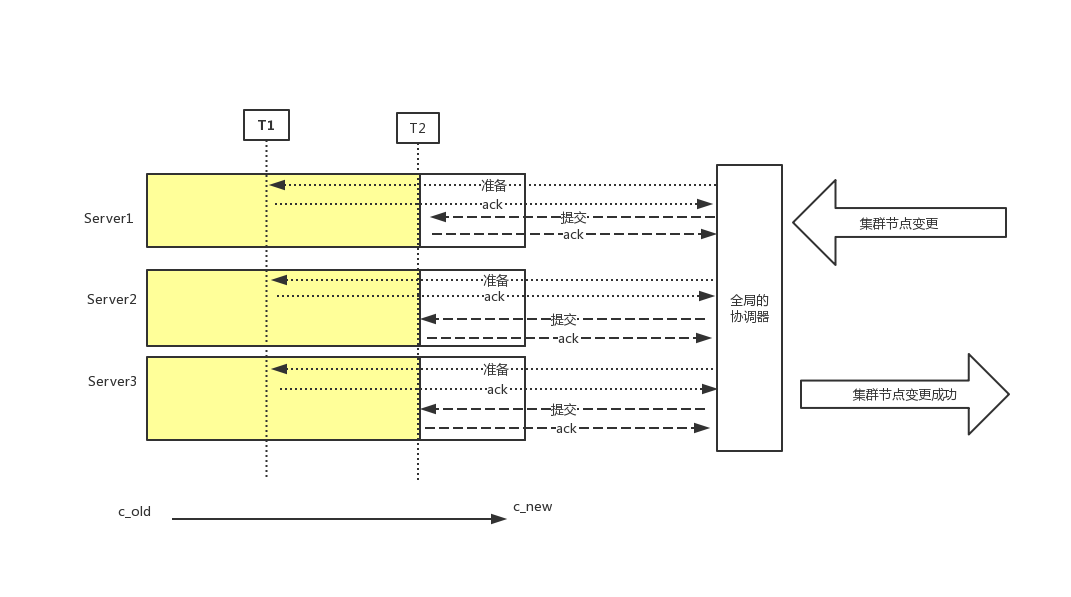
T1阶段各个server收到节点变更消息(各个server)

raft采用如下规则来解决上面问题:

每次一个节点依次加入集群
通过leader来发送集群变更消息,当发送到大多数机器上时leader才将自己从c_old变成c_new

来分析下是如何实现的

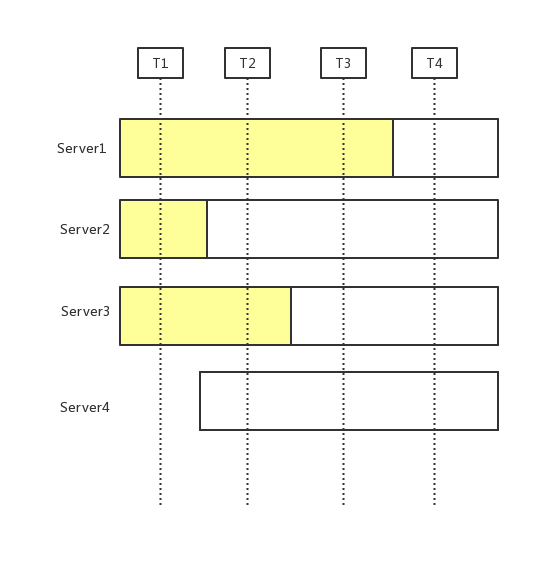
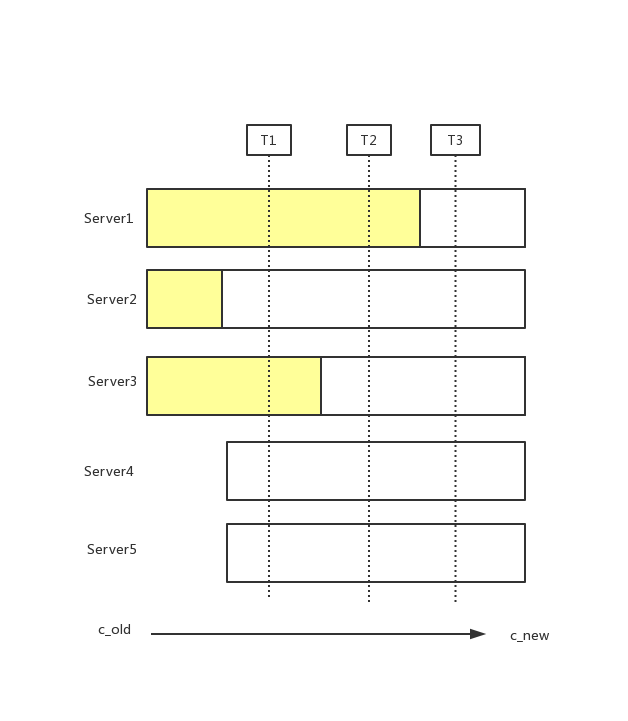
T1时刻, 省略
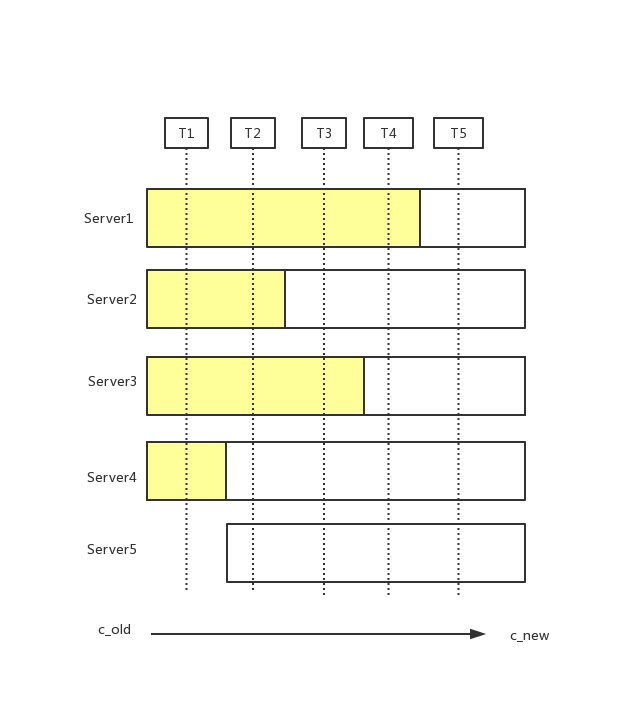
T2时刻,

https://www.jianshu.com/p/99562bfec5c2

https://zhuanlan.zhihu.com/p/56215322

https://zhuanlan.zhihu.com/p/27908888

https://zhuanlan.zhihu.com/p/25344714

集群节点表更,最复杂的情况,从A,B,C变成C,D,E

共同决定的过程

参考文档

Raft算法总结

语法

发表于 2019-12-04 | 分类于 rust

字数统计: | 阅读时长 ≈

https://doc.rust-lang.org/rust-by-example/hello/print.html
https://www.rust-lang.org/learn

1
2
3

:b : 二进制格式
println!("{} of {:b} people know binary, the other half doesn't", 1, 10);
// 1 of 1010 people know binary, the other half doesn't

安装与简介

发表于 2019-12-04 | 分类于 rust

字数统计: | 阅读时长 ≈

初识rust

Rust 是一门系统级编程语言，被设计为保证内存和线程安全，并防止段错误。作为系统级编程语言，它的基本理念是 “零开销抽象”。理论上来说，它的速度与 C / C++ 同级
Rust 使用实现（implementation）、特征（trait）和结构化类型（structured type）而不是类（class）

rust ideal

Rust目前有比较靠谱的IDE吗？
Rust学习笔记

Slice

发表于 2019-12-04 | 分类于 go

字数统计: | 阅读时长 ≈

切片

切片与数组区别
切片在函数之间传递是值传递还是引用传递
append方法是如何进行拷贝的,会产生双倍空间吗
append函数与copy函数不同
子切片修改,会影响父切片的数据
存在的陷阱
Append扩容隐藏的坑

当把slice传给一个函数时，对slice的结构体发生的值传递，而slice中指向数据内容的地址没有变
切片操作并不复制切片指向的元素。它创建一个新的切片并复用原来切片的底层数组。这使得切片操作和数组索引一样高效。因此，通过一个新切片修改元素会影响到原始切片的对应元素
切片操作并不会复制底层的数组。整个数组将被保存在内存中，直到它不再被引用。有时候可能会因为一个小的内存引用导致保存所有的数据,导致 GC 不能释放数组的空间；只用到少数几个字节却导致整个文件的内容都一直保存在内存里,只能通过切片拷贝修复
在使用append()函数给slice中添加元素时，slice的初始大小可以为0，也就是len可以为0。每次向slice中append的时候，如果容量cap不够，会自动对slice进行扩容，也就是改变slice的cap的大小。
而在使用copy()函数操作slice时，如果slice的大小为0时，会不添加任何元素，不会自动增加slice的容量大小。

package main

import (
	"log"
	"testing"
	"unsafe"
)

func init() {
	log.SetFlags(log.Lshortfile | log.LstdFlags)
}

func sliceTest(list []int) {
	if len(list) > 0 {
		log.Println("func pos 0:", &list[0])
	}

	log.Println("func pointer:", unsafe.Pointer(&list))
	log.Println("------")
}

func copyTest() {
	list := make([]int, 0)
	log.Println("pointer:", unsafe.Pointer(&list))
	sliceTest(list)
	log.Println("++++++++++++++")

	list = append(list, 1)
	log.Println("pos 0:", &list[0])
	log.Println("pointer:", unsafe.Pointer(&list))
	sliceTest(list)
	log.Println("++++++++++++++")

	list = append(list, 1, 3, 4, 5)
	log.Println("pos 0:", &list[0])
	log.Println("pointer:", unsafe.Pointer(&list))
	list2 := list
	log.Println("pointer:", unsafe.Pointer(&list2))
	log.Println("pos 0:", &list2[0])
	list3 := list[3:]
	log.Println("pos 1:", &list[0])
	log.Println("pos 1:", &list[1])
	log.Println("pos 1:", &list[2])
	log.Println("pos 1:", &list[3])
	log.Println("pos 1:", &list[4])
	log.Println("pointer:", unsafe.Pointer(&list3))
	log.Println(list3)
	log.Println(list)
	log.Println("pos 0:", &list3[0])
	log.Println("pos 0:", &list3[1])
	log.Println("cap",cap(list3))
	log.Println("cap",len(list3))
	list3[0] = 8
	log.Println(list)
	log.Println(list3)
	list3 = nil
	log.Println(list)
	log.Println(list3)
	log.Println("++++++++++++++")

	list = append(list, 2)
	log.Println("pos 0:", &list[0])
	log.Println("pointer:", unsafe.Pointer(&list))
	sliceTest(list)
	log.Println("++++++++++++++")

	copy1 := make([]int, 0)
	copy(copy1, list)
	log.Println("copy1:", copy1)

	copy2 := make([]int, 2)
	copy(copy2, list)
	log.Println("copy2:", copy2)

	copy3 := make([]int, 0, 2)
	copy(copy3, list)
	log.Println("copy3:", copy3)
	log.Println()
}

func Test(t *testing.T) {
	copyTest()
}

append vs copy

package append_vs_copy

import (
	"testing"
)

func TestCopy(t *testing.T) {
	y := doCopy(true, false)
	if len(y) != 1000 {
		t.Fatalf("Expected len(y) to be 1000 but was %d", len(y))
	}
}

func TestAppend(t *testing.T) {
	y := doCopy(false, false)
	if len(y) != 1000 {
		t.Fatalf("Expected len(y) to be 1000 but was %d", len(y))
	}
}

func TestAppendAlloc(t *testing.T) {
	y := doCopy(false, true)
	if len(y) != 1000 {
		t.Fatalf("Expected len(y) to be 1000 but was %d", len(y))
	}
}

func doCopy(useCopy bool, preAlloc bool) []int64 {
	existing := make([]int64, 1000, 1000)
	var y []int64
	if useCopy {
		y = make([]int64, 1000, 1000)
		copy(y, existing)
	} else {
		var init []int64

		if preAlloc {
			init = make([]int64, 0, 1000)
		} else {
			init = []int64{}
		}
		y = append(init, existing...)
	}
	return y
}

func BenchmarkAppend(b *testing.B) {
	for i := 0; i < b.N; i++ {
		doCopy(false, false)
	}
}

func BenchmarkAppendAlloc(b *testing.B) {
	for i := 0; i < b.N; i++ {
		doCopy(false, true)
	}
}

func BenchmarkAppendAllocInline(b *testing.B) {
	for i := 0; i < b.N; i++ {
		existing := make([]int64, 1000, 1000)
		var init []int64

		init = make([]int64, 0, 1000)
		_ = append(init, existing...)
	}
}

func BenchmarkCopy(b *testing.B) {
	for i := 0; i < b.N; i++ {
		doCopy(true, true)
	}
}